For those of you who don’t watch cricket, or even know what it is, it is often described to novices as an 11-a-side bat and ball game that lasts up to 5 days, sometimes ending in a draw.  For cricket followers, though, a 5 day test match is a chance to immerse yourself in the ebbs and flows of cricketing tension and to discuss endless batting and bowling statistics.

So, to the Ashes – the pre-eminent cricket series played between England and Australia and dating back to 1882.  We’re currently 4 tests into the 2010-11 series, England have won two tests, Australia one and one has been drawn.  This means that, even with one test to go,  England retain the Ashes for the first time in a generation.  In four test matches of two innings for each team, England have scored around 2,000 runs with batsmen getting anything from zero to a massive 235 runs (Alastair Cook in the Brisbane Test).

Now, cricket is an intensely strategic sport.  The decision of whether to bat or bowl after the toss of the coin on the first day can decide the whole series.  And that’s just the start of it: how do you deploy your fielders; when do you use your spinners or your seam bowlers; how will the state of the cracks in the pitch affect the bounce (I’ve supervised not one but two PhDs in this area)?

So, how surprised was I to find that all that has gone on in the Ashes down the years can be boiled down to one law – Benford’s Law, first postulated by Simon Newcomb just one year before the first Ashes series 130 years ago?

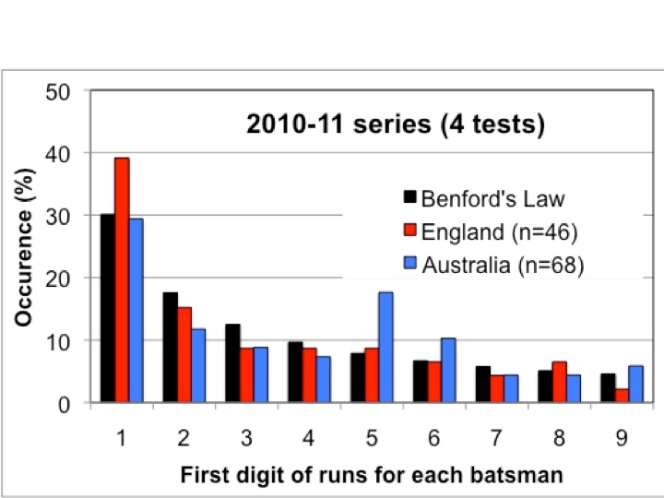
Sometimes called the ‘first digit phenomenon’ Benford’s Law (named after Frank Benford following his 1938 paper) can be applied to large lists of numbers such as cricket scores, the stock market, voting patterns and even the number of lightning strikes per day.  The law says that if we look at the first digit of each number in a list (not including zero), then the distribution of these digits will always be the same.  The digit ‘1’ will always lead 30.1% of the time, digit ‘2’ 17.6% of the time, digit ‘3’ 12.5% of the time and so on.  The distribution for 1 to 9 are shown in Figure 1.

Taking the example of The Ashes, consider the runs in England’s 1st innings at Brisbane in Table 1.   The digit 1 leads twice, 2 leads once, 4 twice, and 6 and 7 once.  If we do this for all innings and tests for England and Australia separately, then we can compare the 2010-11 Ashes scores with Benford’s law (Figure 2).

Given the human endeavour that goes into a cricket game (and indeed any sporting occasion), it is surprising that our efforts can be described by something as simple as the % occurence of the numbers 1 to 9.  Of course, there are some differences between the cricket scores and Benford’s law:  the digit 1 occurs more often than expected for England due to a lot of scores in the teens in the 3rd test; equally the digit 5 occurs more often than expected for Australia due to a larger number of scores in the 50s, particularly in the 2nd test.

Given the small sample of data we are using (n=46 for England; n=68 for Australia) there is probably not enough data to do a good comparison and we might consider that all this has occurred by chance.  Out of interest, I went back to the first Ashes series in 1882-3 to see if anything similar occurred (Figure 3);  again, the distribution follows Benford’s law pretty well apart from the preponderance of 2s for England due to a lot of scores in the 20s.

To me, the whole thing is all a bit mind-blowing.  I spend a lot of time working on sophisticated projects to influence performance in sport, and yet here is a mathematical technique that seems to describe pretty simply a game as complex as cricket over a 130 year span.

So, how can we use it?  It could be used for almost anything number related; in cricket that could be runs per over, runs per batsman, overs per hour.  In other spheres, Benford’s law is used is to detect unusual behaviour, such as voting irregularities and stock market fraud.  Given the occasional accusations of cheating in cricket, perhaps we should use it for that?